Over Memorial Day weekend I took my toy Euchre AI that plays using Information Set Monte Carlo Tree Search and ran it on a VPS with 20 CPUs and recorded the first level of child nodes (which presumably contained all the best moves). There are 42,504 (24 choose 5) Euchre hands. To cut down on computations required I actually skipped hands that had the same set of "outside" cards the second time they were encountered and filled in the details from the previous run that had the same outside cards (with the suits swapped). This reduced the possible number of hands from 42,504 to 22,398. I kept track of each unique hand based on trump (which for the simulations I always kept as hearts) and diamonds (because the distribution of cards in the suit with the same color as trump is different because the jack of the same color becomes the left bower). But for these outside hands I assumed the results would be the same. For example if you have an outside ace and 10 in one suit and and outside jack and queen in the other suit your chances of winning are the same either way.
Monte Carlo Tree Search is a very simple algorithm. In order to use it you need to implement the game rules including a method that returns legal plays that can be made given a game state. MCTS searches the game tree depth-first which means it plays games over and over again to completion from the state it started with. Each time it visits a node where not all the moves have been tried it randomly picks a move it has not yet tried. (This step can be made smarter if you add some heuristics and/or deep learning to prune out suboptimal moves.) If all the moves have been tried it uses an equation to choose which play it should try next. This equation weighs how often it should exploit plays that have led to wins and how often it should explore other moves that appeared to be less optimal but might only have appeared that way.
In order to better understand this equation, called UCT (Upper Confidence Bound 1 applied to Trees), I simulated a game with moves that had a fixed win rate and then graphed the results. The game I simulated is very simple - it has 3 moves. The orange move wins 75% of the time, red 50% and blue 25%. The visits graph is straightforward. UTC exploits the orange (75% win rate) move more often than the red (50% win rate) move and it exploits the blue (25% win rate) move the least:
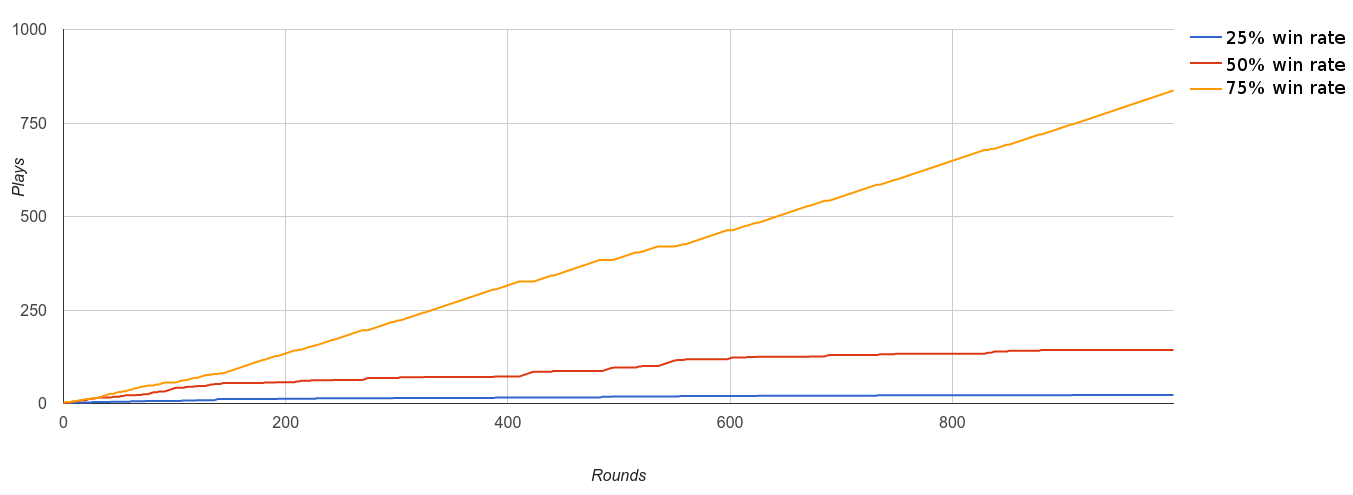
Here is the graph of the UCT values for that same simulation. You can see how it is chaotic at first but then as it figures out that the orange move has a high win rate it visits it more than the others but still checks in with them occasionally.
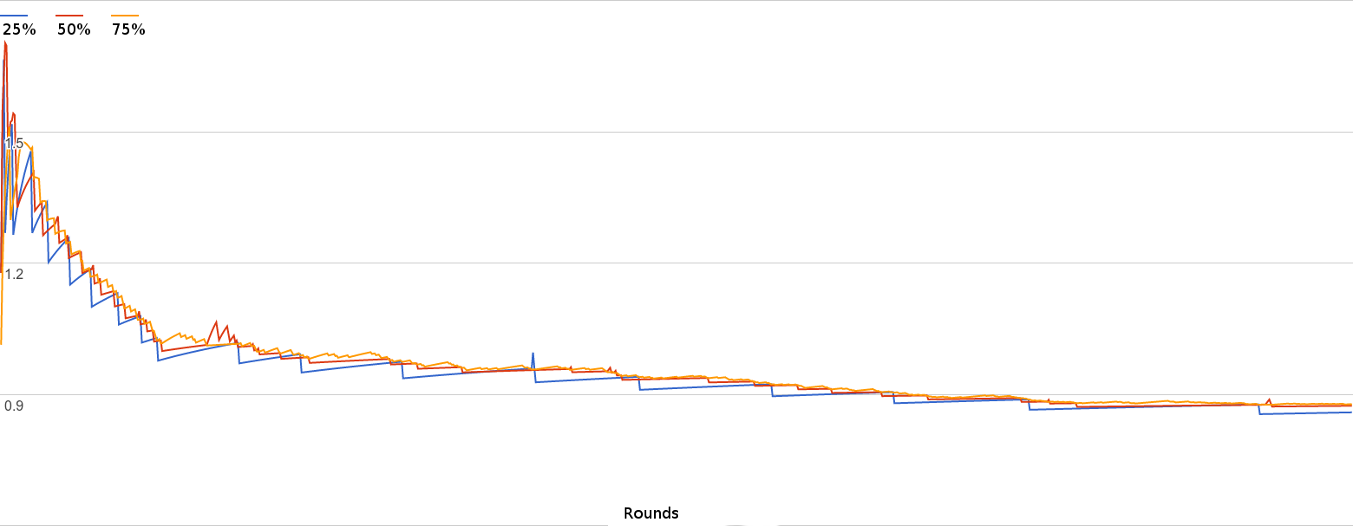
Once its allotted number of runs is done MCTS returns the most visited node as the move to make.
Since Euchre is a game with hidden information I used Information Set Monte Carlo Tree Search which is just a little more complicated than vanilla MCTS. Since you can't be sure which cards your opponents will have for each simulation you randomly distribute cards based on the possible hands a given player could have based on their past play history. So, for example, if a player trumped on spades during the hand their hand must not contain spades (since no cheating is allowed in the simulation).
Here is an example graph from a sample run (with just 1,000 plays) of the Euchre simulation:
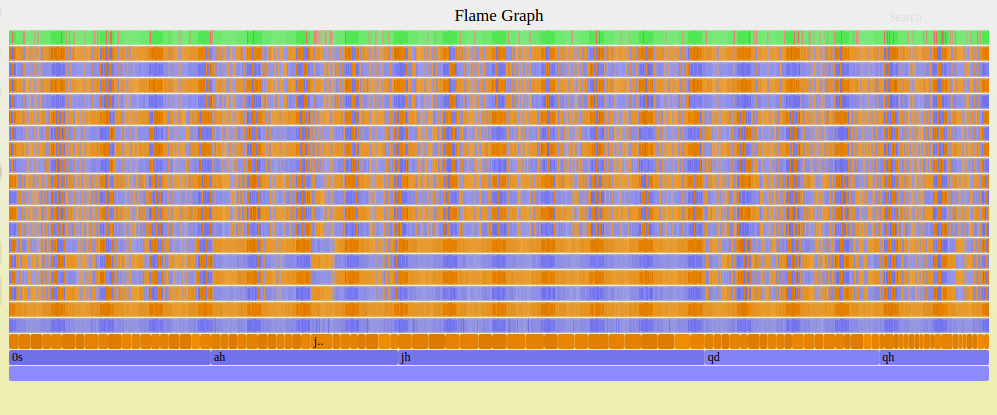
The width of each node represents the number of times it was visited. So for this hand the jack of hearts was the most chosen card and the simulation would choose to play this card first. A green bar in the final row at the top indicates that the blue team (the computer's team) won and a red bar indicates that they lost. This is a strong hand so it wins a lot.
It took about 200 CPU hours (20 CPUs times 10 hours) to complete the simulation for all possible hands though about half way through I realized I had an issue where multiple workers might be working on the same hand so I started writing a flag to to the database before workers took their randomly selected hand. It would have been much better to do this with a queuing system. I love queues so I'm not sure why I did it the way I did - just wanted to keep things simple I guess.
Some random pictures of what was happening on the machine and some random numbers:
| 22,398 de-duplicated hands | (out of 42,504 total hands) |
| 223,980,000 total simulations | (10,000 per hand) |
| 1,119,900,000 total tricks | (5 per simulation) |
| 720,000 CPU seconds | (10 hours) |
| 1555 tricks per second | |
| 311 hands per second | |
| 15.5 hands per second per core |
I got this notice right after I started the simulation (well before 2 hours had passed):
Your node has exceeded the notification threshold (90) for CPU Usage by averaging 1597.0% for the last 2 hours.
To be honest 311 hands per second across 20 cores is pretty pathetic (or my math could be totally wrong). Either way I probably could have made it much more efficient if I put some effort into profiling and optimizing before running this experiment. Catching the potential duplicate work issue faster would have also probably decreased the overall time.
To sanity check the database I looked through a bunch of the top search results for card leading strategies in Euchre. A lot of this strategy deals with situations that this simulation wasn't aware of, like whether or not your partner called up trump. It just starts in a situation where trump is known and everyone has 5 cards to play and it has the lead. One article in particular had some great advice that seems to line up with the database:
Generally speaking, it's worth leading the right bower here if you have it. Yes, you may theoretically be stepping on your partner's left bower, but you can't know for sure, and if you are long in trump then it's a good idea to guarantee yourself this trick, as well as more remaining trump than anyone else at the table.
This is correct! When we query the database we see that out of all hands that had the right bower we see that it is the number one recommended card to play in 3552 total hands with the next highest being the ace of clubs which is the recommended lead for 852 hands.
Lead with a singleton off-suit ace, if you have one. A singleton ace is a strong lead for two reasons. First of all, if no other cards of that suit are in your hand, there is a higher probability that they are in your opponents' hands, preventing them from trumping your ace. Your best chance for an ace to make it around the table and win a trick is on the opening lead.
Pay special attention to the "next" suit, the same-color suit as trump. Since the left bower switches suits, this suit only has five cards, and thus even if you hold only an ace and one other card in that suit, leading the ace will often be an invitation for your opponents to trump you.
In this case, save your ace for later and hope it can win a trick once trump is all drawn out.
This website is 2/2. This is totally backed up by the simulation. Here is a hand with a singleton ace.
So I paid about 10 dollars to run a 20 core VPS for 10 hours to be just a little bit more confident that what we already knew about Euchre was correct. Ah well - it was fun nonetheless. Maybe someone else can find more interesting information in the database. It's available on GitHub. And you can query it on euchredb.bravender.net.